Correlation Factor Calculator

To find the correlation factor (r), sum the products of the deviations of each value from the mean for two datasets, then divide by the product of the standard deviations of each dataset. This calculation gives the degree of linear relationship between two variables.

Correlation Factor Calculator

X Values (comma-separated) Y Values (comma-separated) Correlation Factor

Calculate Reset

The Correlation Factor Calculator is a statistical tool that is applied to measure the strength and direction of the linear relationship between two variables. This is especially valuable in fields like finance, biology, and social sciences, where understanding the relationship between variables helps in decision-making and data analysis.

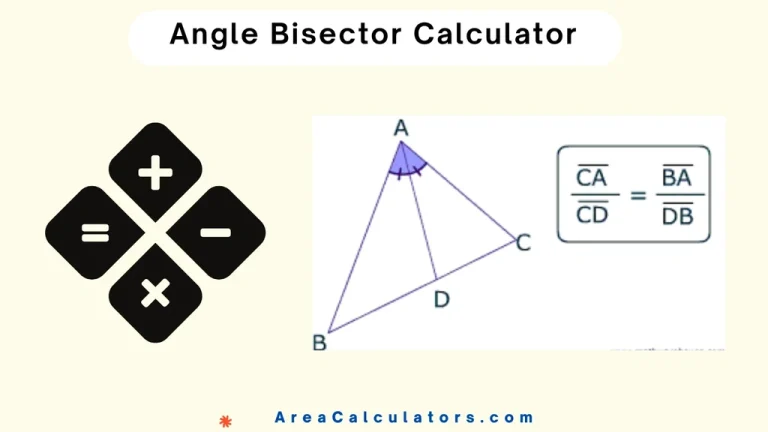
The correlation factor, often represented by $r$, ranges between -1 and 1. A positive value indicates a positive relationship, while a negative value shows an inverse relationship. Calculating the correlation helps analysts understand trends, predict outcomes, and identify associations between data points.

Formula:

$$r = \frac{\Sigma[(x_i – \bar{x})(y_i – \bar{y})]}{\sqrt{\Sigma(x_i – \bar{x})^2} \times \sqrt{\Sigma(y_i – \bar{y})^2}}$$

Variable	Description
$r$	Correlation Factor (correlation coefficient)
$x_i$	Individual values in the first dataset
$y_i$	Individual values in the second dataset
$\bar{x}$	Mean of the first dataset
$\bar{y}$	Mean of the second dataset

Solved Calculations

Example 1:
Consider two datasets, $X = \{2, 4, 6, 8\}$ and $Y = \{5, 9, 11, 13\}$ . Calculate the correlation factor.

Step	Calculation
1.	Find the means $\bar{x} = 5$ and $\bar{y} = 9.5$
2.	Calculate $(x_i – \bar{x})(y_i – \bar{y})$ and sum
3.	Calculate $\Sigma(x_i – \bar{x})^2$ and $\Sigma(y_i – \bar{y})^2$
4.	$r = \frac{\Sigma[(x_i – \bar{x})(y_i – \bar{y})]}{\sqrt{\Sigma(x_i – \bar{x})^2} \times \sqrt{\Sigma(y_i – \bar{y})^2}}$
5.	Answer: $r = 0.94$

Example 2:
For datasets $X = \{10, 12, 14\}$ and $Y = \{20, 25, 30\}$ :

Step	Calculation
1.	Find the means $\bar{x}=12$ and $\bar{y} = 25$
2.	Calculate $(x_i – \bar{x})(y_i – \bar{y})$ and sum
3.	Calculate $\Sigma(x_i – \bar{x})^2$ and $\mathrm{\Sigma }(y_i-\bar{y}{)}^2$
4.	$r = \frac{\Sigma[(x_i – \bar{x})(y_i – \bar{y})]}{\sqrt{\Sigma(x_i – \bar{x})^2} \times \sqrt{\Sigma(y_i – \bar{y})^2}}$
5.	Answer: $r = 1.0$

What is a Correlation Factor Calculator?

The Correlation Factor Calculator is a tool that is commonly used in statistical field. It comes handy when calculating the relationship strength between two variables by calculating the correlation coefficient.

This tool is widely used in statistics and data analysis to understand how changes in one variable might be associated with changes in another.

For example, the Pearson Correlation Coefficient (often symbolized as “r”) is one of the most common measures, indicating how strongly variables are linearly related.

Using this calculator, you can quickly find the correlation factor with ease. Simply input the data values, and the calculator provides the correlation coefficient, helping you interpret if the relationship is positive, negative, or neutral. This tool is useful for research, business analysis, and academic studies, as it offers insight into patterns and trends in data.

Final Words:

At last, the Correlation Factor Calculator is fundamental for assessing relationships between variables, providing valuable data insights that guide decision-making in various fields.